记录机器学习深度学习算法

1. 基础

1.1 ROC计算过程

ROC全称是“受试者工作特征”（Receiver Operating Characteristic）。ROC曲线的面积就是AUC（Area Under the Curve）。AUC用于衡量“二分类问题”机器学习算法性能（泛化能力）。

Python中sklearn直接提供了用于计算ROC的函数，下面就把函数背后的计算过程详细讲一下。

1.1.1 一些概念

计算ROC需要知道的关键概念，首先，解释几个二分类问题中常用的概念：

True Positive, False Positive, True Negative, False Negative。

它们是根据真实类别与预测类别的组合来区分的。假设有一批test样本，这些样本只有两种类别：正例和反例。机器学习算法预测类别如下图（左半部分预测类别为正例，右半部分预测类别为反例），而样本中真实的正例类别在上半部分，下半部分为真实的反例。

预测值为正例，记为P（Positive）
预测值为反例，记为N（Negative）
预测值与真实值相同，记为T（True）
预测值与真实值相反，记为F（False）

	预测值
真实值	正例	反例
正例	TP	FN
反例	FP	TN

TP：预测类别是P（正例），真实类别也是P
FP：预测类别是P，真实类别是N（反例）
TN：预测类别是N，真实类别也是N
FN：预测类别是N，真实类别是P

样本中的真实正例类别总数即TP+FN。TPR即True Positive Rate，TPR = TP/(TP+FN)。

同理，样本中的真实反例类别总数为FP+TN。FPR即False Positive Rate，FPR=FP/(TN+FP)。

还有一个概念叫”截断点”。机器学习算法对test样本进行预测后，可以输出各test样本对某个类别的相似度概率。比如t1是P类别的概率为0.3，一般我们认为概率低于0.5，t1就属于类别N。这里的0.5，就是”截断点”。

总结一下，对于计算ROC，最重要的三个概念就是TPR, FPR, 截断点。截断点取不同的值，TPR和FPR的计算结果也不同。将截断点不同取值下对应的TPR和FPR结果画于二维坐标系中得到的曲线，就是ROC曲线。横轴用FPR表示。

1.1.2 sklearn计算ROC

sklearn给出了一个计算ROC的例子。

1
2
3

y = np.array([ 1, 1, 2, 2])
scores = np.array([ 0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label= 2)

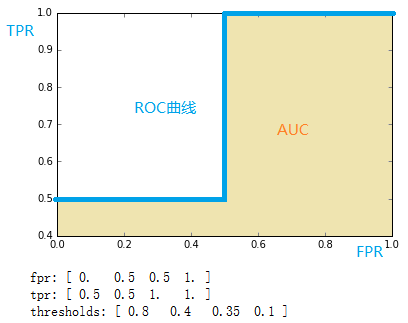
通过计算，得到的结果（TPR, FPR, 截断点）为

1
2
3

fpr = array([ 0., 0.5, 0.5, 1.])
tpr = array([ 0.5, 0.5, 1., 1.])
thresholds = array([ 0.8, 0.4, 0.35, 0.1]) #截断点

将结果中的FPR与TPR画到二维坐标中，得到的ROC曲线如下（蓝色线条表示），ROC曲线的面积用AUC表示（淡黄色阴影部分）。

1.1.2.1 详细计算过程

上例给出的数据如下

1 2	y = np.array([ 1, 1, 2, 2]) scores = np.array([ 0.1, 0.4, 0.35, 0.8])

用这个数据，计算TPR，FPR的过程是怎么样的呢？

1.1.2.1.1 分析数据

y是一个一维数组（样本的真实分类）。数组值表示类别（一共有两类，1和2）。我们假设y中的1表示反例，2表示正例。即将y重写为：

y_true = [ 0, 0, 1, 1]

score即各个样本属于正例的概率。

1.1.2.1.2 针对score，将数据排序

样本	预测属于P的概率(score)	真实类别
y[0]	0.1	N
y[2]	0.35	P
y[1]	0.4	N
y[3]	0.8	P

1.1.2.1.3 将截断点依次取为score值

将截断点依次取值为0.1,0.35,0.4,0.8时，计算TPR和FPR的结果。

截断点为0.1

说明只要score>=0.1，它的预测类别就是正例。

此时，因为4个样本的score都大于等于0.1，所以，所有样本的预测类别都为P。

1
2
3

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1]
y_pred = [1, 1, 1, 1]

	预测值
真实值	正例	反例
正例	TP=2	FN=0
反例	FP=2	TN=0

1 2	TPR = TP/(TP+FN) = 1 FPR = FP/(TN+FP) = 1

截断点为0.350

说明只要score>=0.35，它的预测类别就是P。

此时，因为4个样本的score有3个大于等于0.35。所以，所有样本的预测类有3个为P（2个预测正确，1一个预测错误）；1个样本被预测为N（预测正确）。

1
2
3

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1]
y_pred = [0, 1, 1, 1]

	预测值
真实值	正例	反例
正例	TP=2	FN
反例	FP=1	TN=1

1 2	TPR = TP/(TP+FN) = 1 FPR = FP/(TN+FP) = 0.5

截断点为0.4

说明只要score>=0.4，它的预测类别就是P。

此时，因为4个样本的score有2个大于等于0.4。所以，所有样本的预测类有2个为P（1个预测正确，1一个预测错误）；2个样本被预测为N（1个预测正确，1一个预测错误）。

1
2
3

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1]
y_pred = [0, 1, 0, 1]

	预测值
真实值	正例	反例
正例	TP=1	FN=1
反例	FP=1	TN=1

1 2	TPR = TP/(TP+FN) = 0.5 FPR = FP/(TN+FP) = 0.5

截断点为0.8

说明只要score>=0.8，它的预测类别就是P。所以，所有样本的预测类有1个为P（1个预测正确）；3个样本被预测为N（2个预测正确，1一个预测错误）。

1
2
3

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1]
y_pred = [0, 0, 0, 1]

	预测值
真实值	正例	反例
正例	TP=1	FN=1
反例	FP=0	TN=2

1 2	TPR = TP/(TP+FN) = 0.5 FPR = FP/(TN+FP) = 0

1.1.3 总结

TPR：真实的正例中，被预测正确的比例
FPR：真实的反例中，被预测正确的比例

最理想的分类器，就是对样本分类完全正确，即FP=0，FN=0。所以理想分类器TPR=1，FPR=0。

2. 算法研究

2.1 XGBoost

2.1.1 概述

在这里,我们首先来看一看XGBoost训练完成之后的具体结果.在sklearn实现的xgboost中我们可以将每一棵树的结果绘制出来,具体的代码参考这里 .

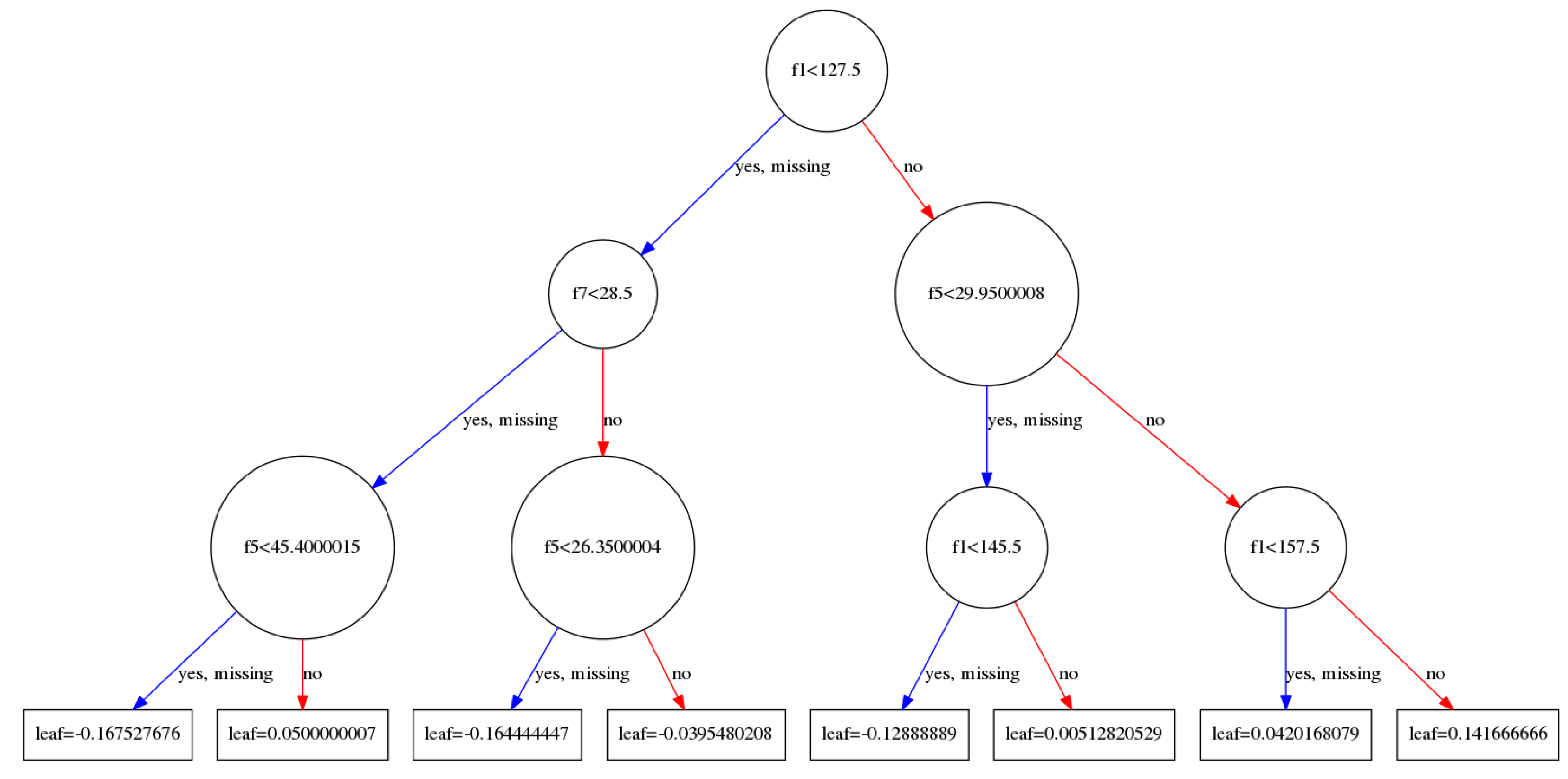
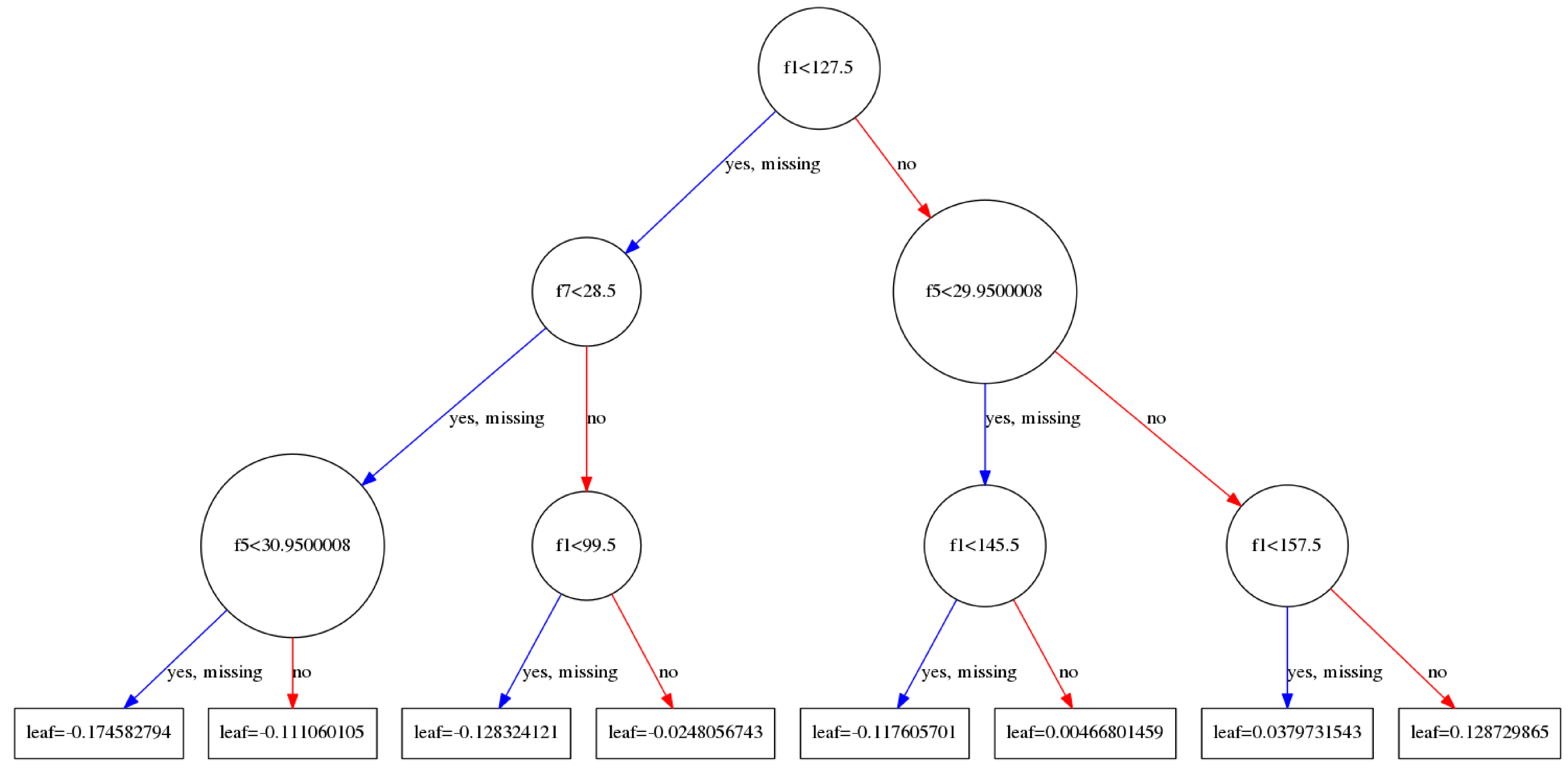
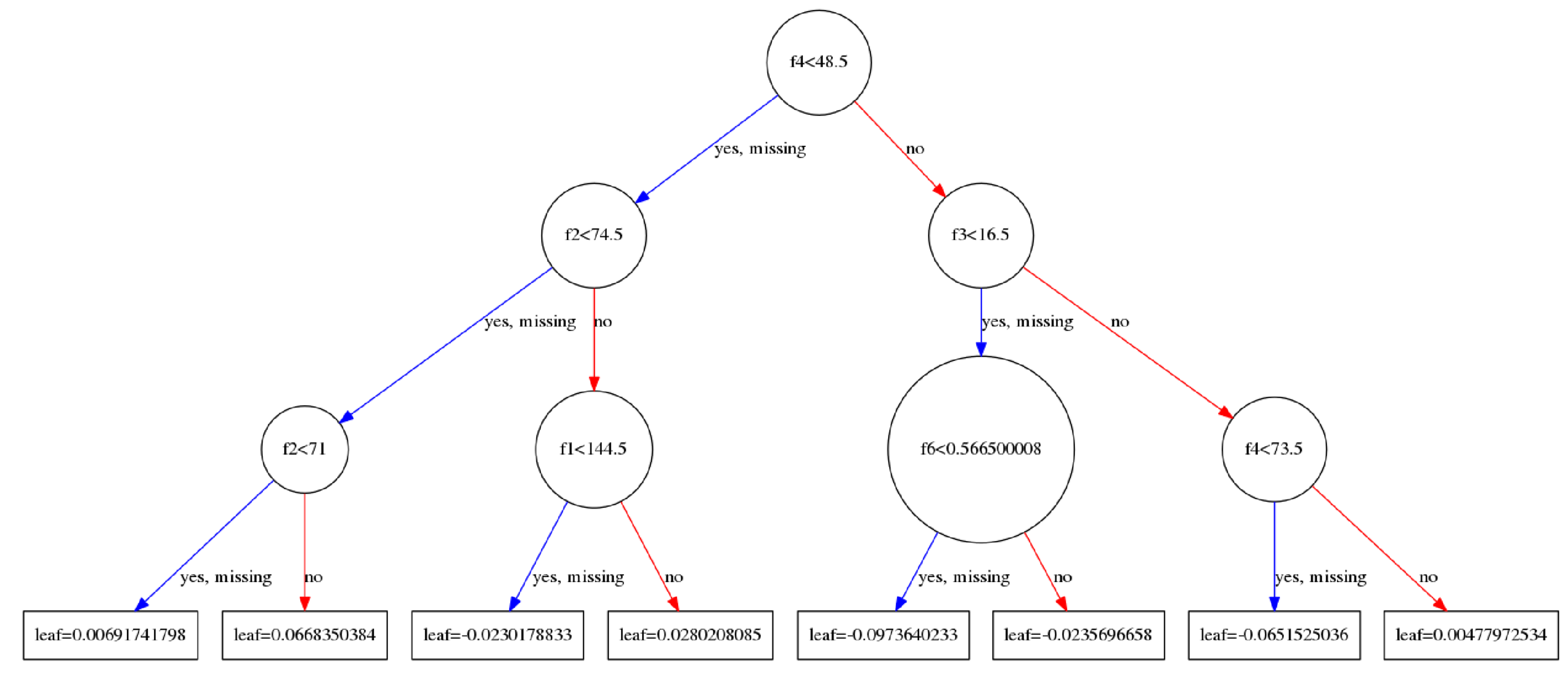
不惜篇幅画了这三张图,依次分别是tree_0,tree_1,tree_99.每一棵树的建立都是依赖于前一棵树建立起来的.

对于当前一棵树的建立:主要的过程是在寻找使用哪一个特征以及这一个特征的哪一个取值来进行分割当前节点上所有的样本(注意并非全部样本,样本在父节点上都已经分割过多次的).当前的节点会计算出一个权重值,这个权重$w$将会被用作更新$\hat{y_i}^{(t-1)}$,$\hat{y_i}^{(t-1)}$被用来计算损失loss,通过loss又来计算一阶导数,二阶导数,通过一阶导数以及二阶倒数又来更新新的$w$,最后的叶子节点将会计算出一个权重值保存.
串行执行是如何实现的呢?答案很容易理解,建立完成一棵树以后,在建立下一棵树的时候,是需要利用已经建立好的树来计算$\hat{y_i}^{(t-1)}$的,这个值又被用来计算残差$y_i-\hat{y_i}^{(t-1)}$,残差是loss的一个组成部分,同时是求解导数所必须的(求导很简单,因为算是函数都是那么集中,如均方误差等,导数有解析解,套上数据就行了).我们发现,新的树的建立依赖于已经建立好的树来参与计算.
需要注意,一个特征在分割的时候并不是只使用一次,在xgboost中,每一个节点的分割都是遍历了所有的特征,使用贪心算法来进行分割的时候,还遍历了排好序的所有的取值,不过在近似处理的时候是对排好序的数据进行分桶后处理,算法的细节稍后讨论.

2.1.2 warning: math

下面来谈论一下xgboost的数学细节,对于论文中出现的公式来进行逐个分析:

Equ 1 :串行添加函数,当前的结果是所有函数计算结果的累加. $\hat{y_i}=\phi(x_i)=\sum_{k=1}^{K}f_k(x_i),f_k \in F$
Equ 2 :损失是两部分构成的,一部分是当前的残差,另外的一部分是限制添加的函数的复杂度的. $L(\phi)=\sum_{i}l(\hat{y_i},y_i)+\sum_{k}\Omega(f_k)$ where $\Omega(f)=\gamma T+\frac{1}{2}\lambda | w |^2$

当前的预测值可以被拆分成为两部分,一部分是前面所有函数的计算结果的累加,另外一部分是当前函数的计算结果.

$L(\phi)=\sum_{i}l(y_i,\hat{y_i}^{t-1}+f_t(x_i))+\sum_{k}\Omega(f_k)$

将$L(\phi)$使用泰勒公式展开,得到(就是新加入的函数$f_t(x)$是增量):

$L^{(t)}\simeq \sum_{i=1}^{n}[l(y_i,\hat{y}^{(t-1)})+g_if_t(x_i)+\frac{1}{2}h_i f_t^2(x_i)]+\Omega(f_t)$

where $gi=\partial{\hat{y}^{t-1}}l(yi,\hat{y}^{t-1})$(一阶导数),$h_i=\partial^2{\hat{y}^{t-1}}l(y_i,\hat{y}^{t-1})$(二阶倒数).

Equ 3
将常数项省略掉后得到的以下式子: $L^{(t)}\simeq \sum_{i=1}^{n}[g_if_t(x_i)+\frac{1}{2}h_i f_t^2(x_i)]+\Omega(f_t)$
Equ 4 $L^{(t)}\simeq \sum_{i=1}^{n}[g_if_t(x_i)+\frac{1}{2}h_i f_t^2(x_i)]+\gamma T+\frac{1}{2}\lambda \sum_{j=1}^{T}{\| w \|^2}=\sum_{j=1}^{T}[(\sum_{i \in I_j}g_i)w_j+\frac{1}{2}(\sum_{i \in I_j}h_i+\lambda)w_j^2]+\gamma T$
Equ 5
对于上式进行求导,命导数等于0,得到优化后的$w^*$ $w^*=-\frac{\sum_{i \in I_j}g_i}{\sum_{i \in I_j}h_i+\lambda}$
Equ 6
将$w^*$带入计算 $L^{(t)}(q)=-\frac{1}{2}\sum_{j=1}^{T} \frac{(\sum_{i \in I_j}g_i)^2}{\sum_{i\in I_j}h_i+\lambda}+\gamma T$
Equ 7 $L_{split}=\frac{1}{2}[\frac{(\sum_{i \in I_R}g_i)^2}{\sum_{i\in I_R}h_i+\lambda}+\frac{(\sum_{i \in I_L}g_i)^2}{\sum_{i\in I_L}h_i+\lambda}-\frac{(\sum_{i \in I}g_i)^2}{\sum_{i\in I}h_i+\lambda}]-\gamma$

2.1.3 XGBoost相关的参数

2.2 ensemble之初音女神

通过初音案例分析ensemble原理

2.2.1 初音

import matplotlib
import numpy as np
from PIL import Image
from matplotlib.pyplot import imshow

miku = pd.read_csv("../data/miku")
miku = np.array(miku.values)

miku_grayscale = miku[:, 2]

miku_grayscale = miku_grayscale.reshape((500, 500))
miku_grayscale = miku_grayscale.transpose()

image = Image.fromarray(miku_grayscale*255)
print(image.size)
imshow(image)
# image.show()
# np.random.shuffle(miku)
miku_data = miku[:, 0:2]
miku_target = miku[:, 2]

1	(500, 500)

png

2.2.2 Decision Tree

from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()
clf.fit(miku_data, miku_target)
predict = clf1.predict(miku_data)
predict = predict.reshape((500, 500))
predict = predict.transpose()

image_pre = Image.fromarray(predict*255)
# image_pre.show()
imshow(image_pre)

png

2.2.3 Bagging

# bagging
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
# clf = BaggingClassifier(DecisionTreeClassifier(max_depth=5), n_estimators=100)
clf = BaggingClassifier(DecisionTreeClassifier(), n_estimators=100)

clf.fit(miku_data, miku_target)

predict = clf.predict(miku_data)
predict = predict.reshape((500, 500))
predict = predict.transpose()

image_pre = Image.fromarray(predict*255)
# image_pre.show()
imshow(image_pre)

png

2.2.4 Boosting

# adaboost
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
clf1 = AdaBoostClassifier(DecisionTreeClassifier(max_depth=5), n_estimators=10)


clf1.fit(miku_data, miku_target)

predict1 = clf1.predict(miku_data)
predict1 = predict1.reshape((500, 500))
predict1 = predict1.transpose()

image_pre1 = Image.fromarray(predict1*255)
# image_pre.show()
imshow(image_pre1)

png

clf2 = AdaBoostClassifier(DecisionTreeClassifier(max_depth=5), n_estimators=100)
clf2.fit(miku_data, miku_target)
predict2 = clf2.predict(miku_data)
predict2 = predict2.reshape((500, 500))
predict2 = predict2.transpose()
image_pre2 = Image.fromarray(predict2*255)
imshow(image_pre2)

png

2.2.5 GBDT

from sklearn.ensemble import GradientBoostingClassifier
clf3 = GradientBoostingClassifier(max_depth=10,n_estimators=100)
clf3.fit(miku_data, miku_target)
predict4 = clf3.predict(miku_data)
predict4 = predict4.reshape((500, 500))
predict4 = predict4.transpose()

image_pre4 = Image.fromarray(predict4*255)
# image_pre.show()
imshow(image_pre4)

png

2.2.6 XGBoost

import xgboost as xgb
param = {'max_depth':5, 
         'eta':1, 
         'silent':1, 
         'objective':'binary:logistic',
         'n_estimators':10,
        }
num_rounds = 500 # 迭代次数
xgb_train=xgb.DMatrix(miku_data,label=miku_target)
xgb_test=xgb.DMatrix(miku_data)

model = xgb.train(param, xgb_train, num_rounds)

predict3=model.predict(xgb_test)
predict3 = predict3.reshape((500, 500))
predict3 = predict3.transpose()
image_pre3 = Image.fromarray(predict3*255)
imshow(image_pre3)

png

3. 方向研究

迁移学习(Transfer Learning)

Transfer Learning Definition:
Ability of a system to recognize and apply knowledge and skills learned in previous domains/tasks to novel domains/tasks.

相关研究工作

2014年Bengio等人^[1]研究深度学习中各个layer特征的可迁移性（或者说通用性）
戴文渊等人提出的TrAdaBoost算法就是典型的基于实例的迁移。
DANN (Domain-Adversarial Neural Network)^[5]将近两年流行的对抗网络思想引入到迁移学习中

增量学习(Incremental learning)

增量学习作为机器学习的一种方法，现阶段得到广泛的关注。在其中，输入数据不断被用于扩展现有模型的知识，即进一步训练模型，它代表了一种动态的学习的技术。对于满足以下条件的学习方法可以定义为增量学习方法：

可以学习新的信息中的有用信息
不需要访问已经用于训练分类器的原始数据
对已经学习的知识具有记忆功能
在面对新数据中包含的新类别时，可以有效地进行处理

增量学习的分类

序号	类别	备注
1	Sample Incremental Learning
2	Class Incremental Learning
3	Feature Incremental Learning

相关研究工作

《End-to-End Incremental Learning》Although deep learning approaches have stood out in recent years due to their state-of-the-art results, they continue to suffer from catastrophic forgetting, a dramatic decrease in overall performance when training with new classes added incrementally. This is due to current neural network architectures requiring the entire dataset, consisting of all the samples from the old as well as the new classes, to update the model -a requirement that becomes easily unsustainable as the number of classes grows. We address this issue with our approach to learn deep neural networks incrementally, using new data and only a small exemplar set corresponding to samples from the old classes. This is based on a loss composed of a distillation measure to retain the knowledge acquired from the old classes, and a cross-entropy loss to learn the new classes. Our incremental training is achieved while keeping the entire framework end-to-end, i.e., learning the data representation and the classifier jointly, unlike recent methods with no such guarantees. We evaluate our method extensively on the CIFAR-100 and ImageNet (ILSVRC 2012) image classification datasets, and show state-of-the-art performance.^[6]

引用

1.How transferable are features in deep neural networks（NIPS2014 Bengio et al.） ↩
2.Learning and Transferring Mid-Level Image Representations using Convolutional Neural Networks（CVPR2014 Oquab.et al.） ↩
3.Domain Adaptation for Large-Scale Sentiment Classification: A Deep Learning Approach（ICML2011 Glorot. Bengio.et al.） ↩
4.Marginalized denoising autoencoders for domain adaptation (ICML2012 Chen et al.) ↩
5.Domain-Adversarial Training of Neural Networks（JMLR2016 Ganin.et al.） ↩
6.Castro, F. M., Marín-Jiménez, M. J., Guil, N., Schmid, C., & Alahari, K. (2018). End-to-end incremental learning. In Proceedings of the European Conference on Computer Vision (ECCV) (pp. 233-248). ↩